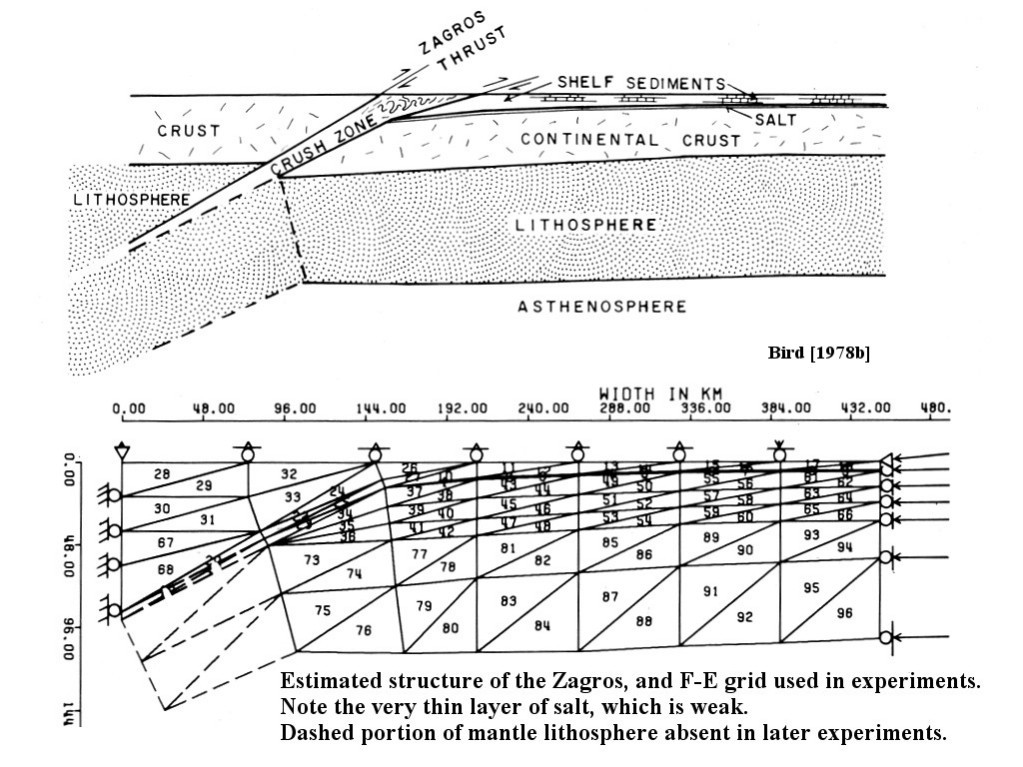
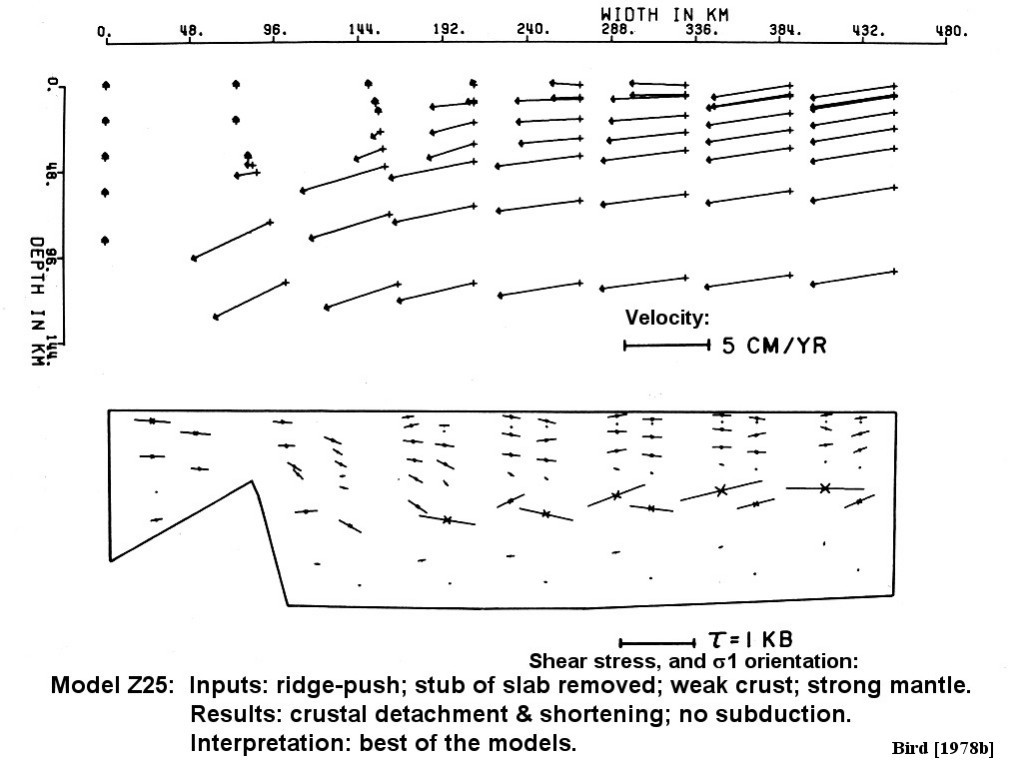
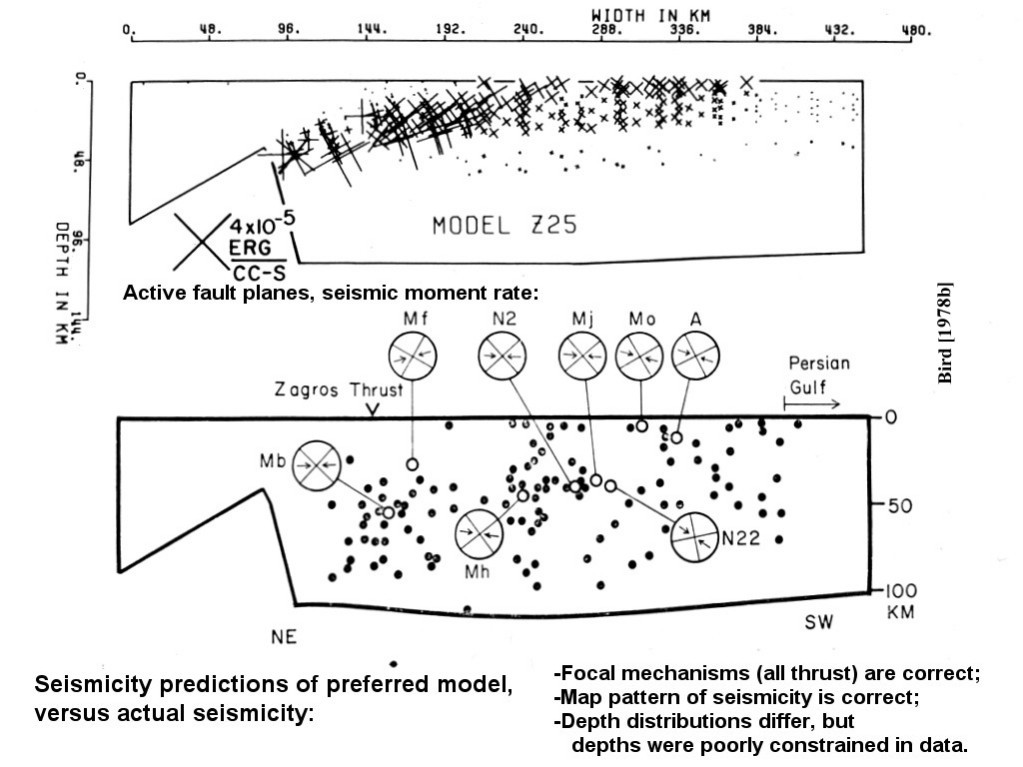
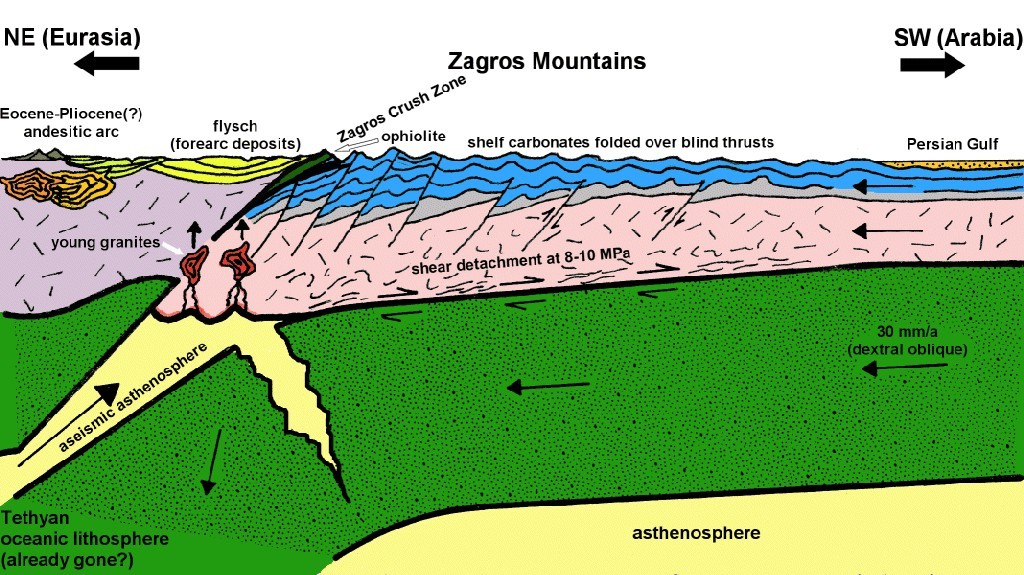
9. Bird, P. (1978b) Finite-element modeling of lithosphere deformation: The Zagros collision orogeny, Tectonophysics, 50, 307-336.

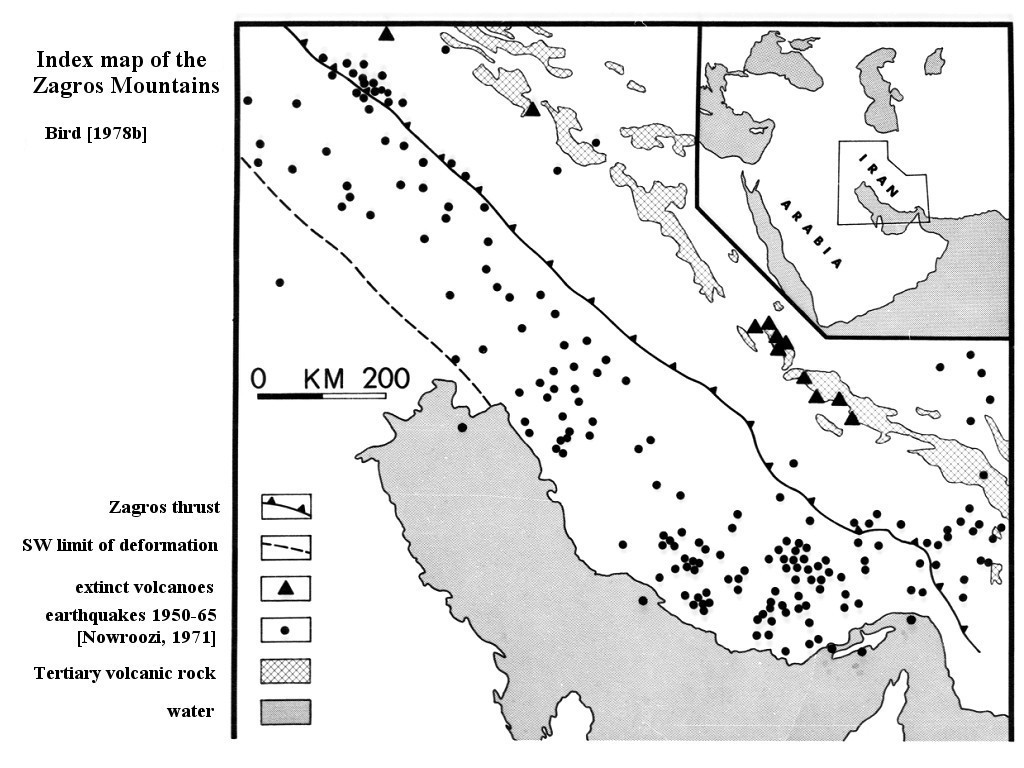
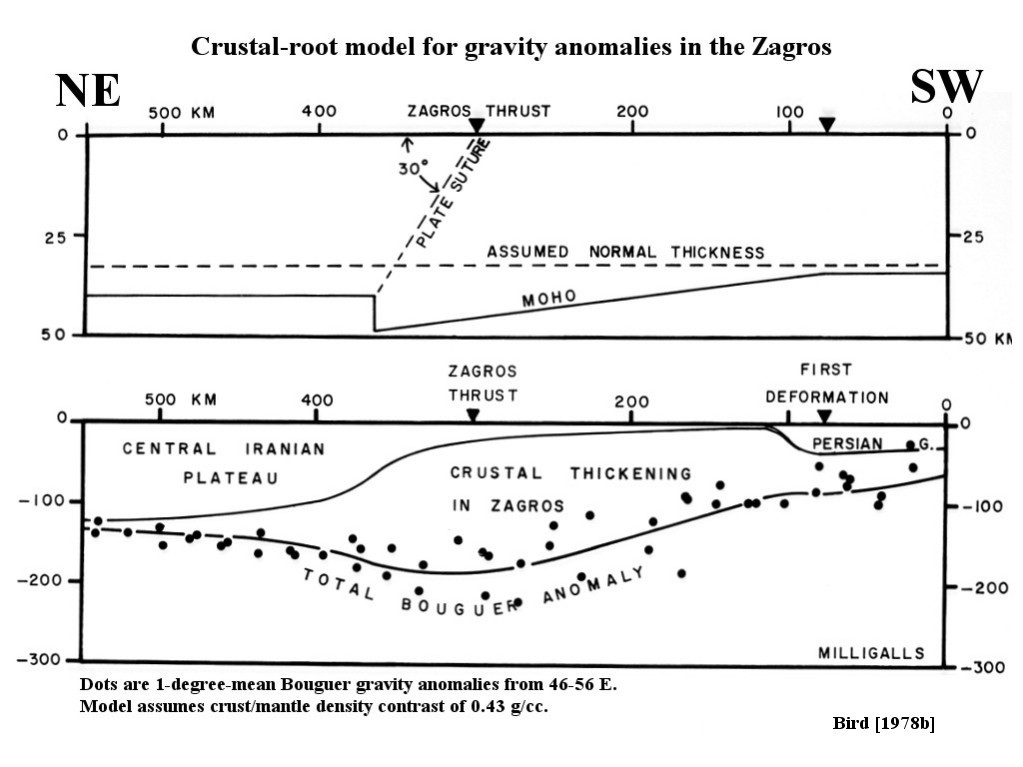
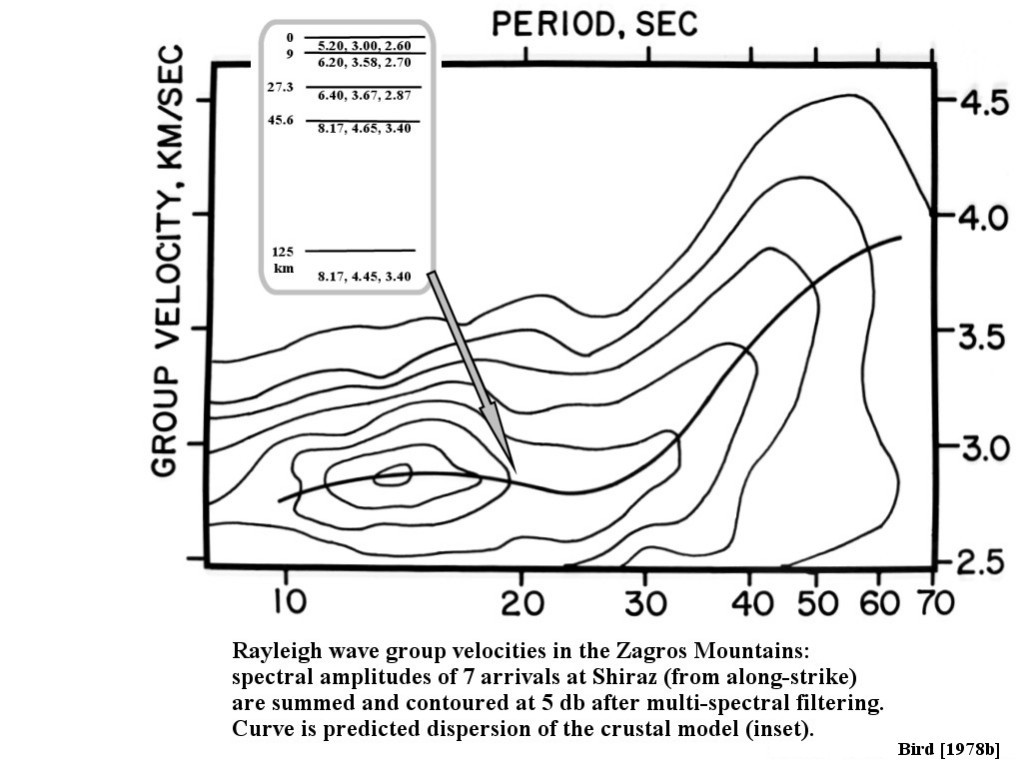
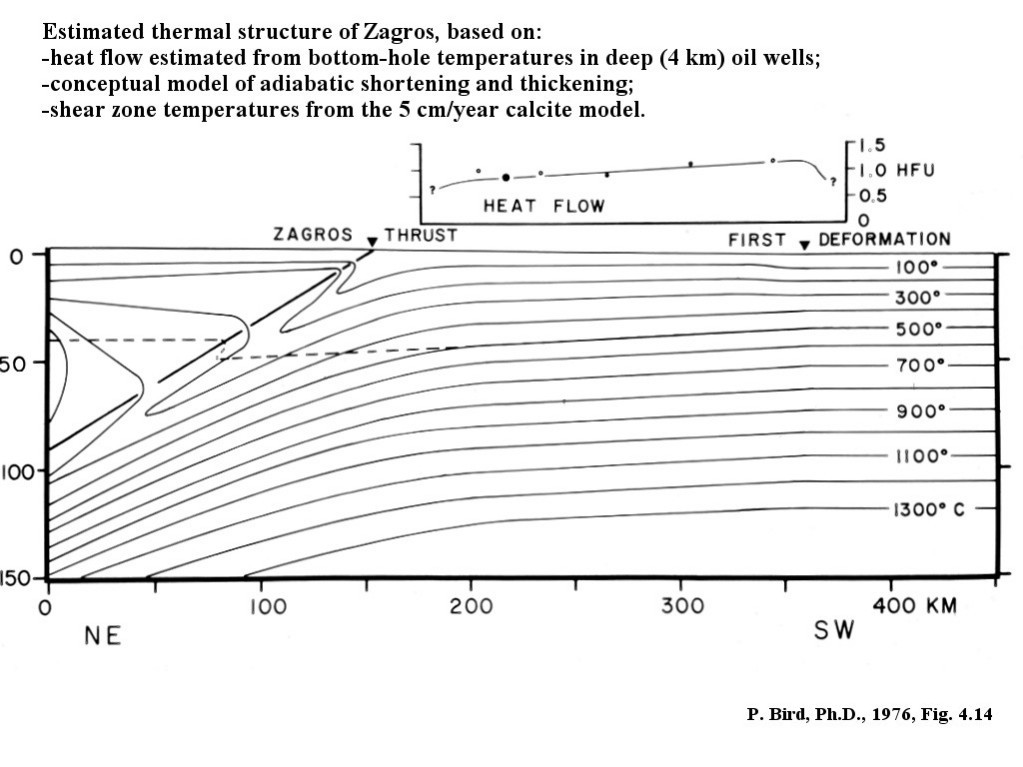
Abstract. In the Zagros Mountains a formerly stable continental margin is being suddenly deformed. Finite element models of this tectonic flow are used to relate known surface deformations, earthquake locations, and fault plane solutions to unknown rock flow parameters and driving forces, in order to determine the latter. These two-dimensional plane-strain flow models incorporate the effects of nonlinear dislocation creep, frictional faulting, geological inhomogeneity, density anomalies, and varying temperature. All models driven by a subducting slab are unsuccessful because they require subduction of continental crust, which does not match present seismicity. Therefore the former oceanic slab must be detached, and the orogeny must be driven by horizontal compression in the lithosphere. Models also show that the subcrustal lithosphere is not shortened but acts as a stabilizing foundation. These results imply a simple geometry of crustal deformation which can be analytically modeled. The creep strength of the lower crust (75-100 bars) determines the topographic slope of the Zagros. The fact that subduction is not occurring on the old plate boundary places a limit on the shear stress deforming the cold upper crust. This limit is 300 bars if there is limestone at depth in the Crush Zone; otherwise 800 bars. These results are confirmed by a final finite element model. The total driving force of the orogeny associated with these limits is 2.8-5.5 ´ 10¹¹ dyne/cm, and the smaller amount could be provided by the gravitational spreading of the Red Sea rift. Shear-strain heating caused by the orogeny to date is less than 20° C. These results imply that even unheated continental crust is considerably weaker than laboratory friction measurements imply, and that it is mechanically decoupled at the Moho from the stronger mantle lithosphere.

P.S. Units are not SI. Convert 75-100 bars = 7.5-10 MPa; 300 bars = 30 MPa; 800 bars = 80 MPa; 2.8-5.5 ´ 10¹¹ dyne/cm = 2.8-5.5 ´ 10¹² N/m. P. Bird, 2000.08.31