72. Bird, P., and M. M. C. Carafa [2016]: Improving deformation models by discounting transient signals in geodetic data, 1: Concept and synthetic examples, J. Geophys. Res., 121(7), 5538-5556, doi: 10.1002/2016JB013056.
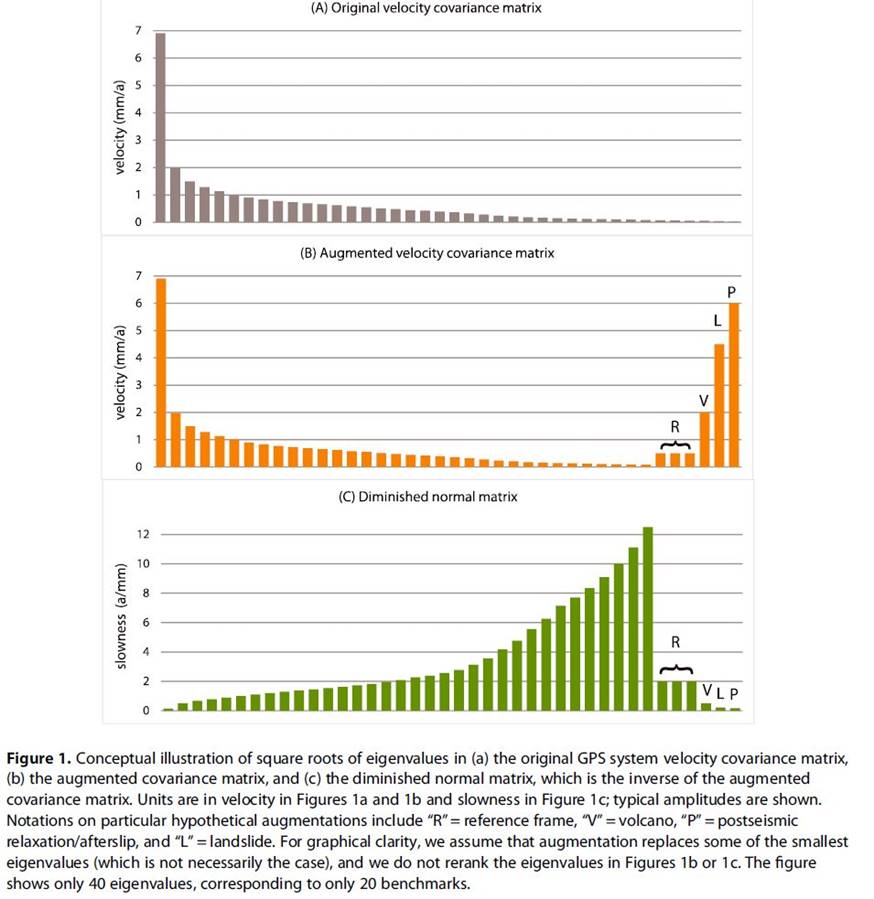
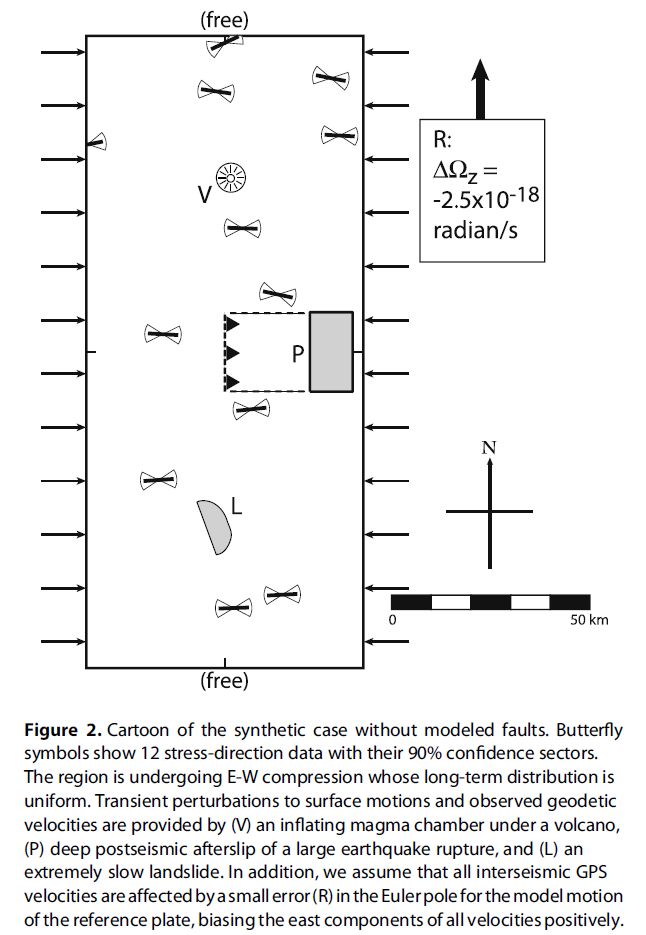
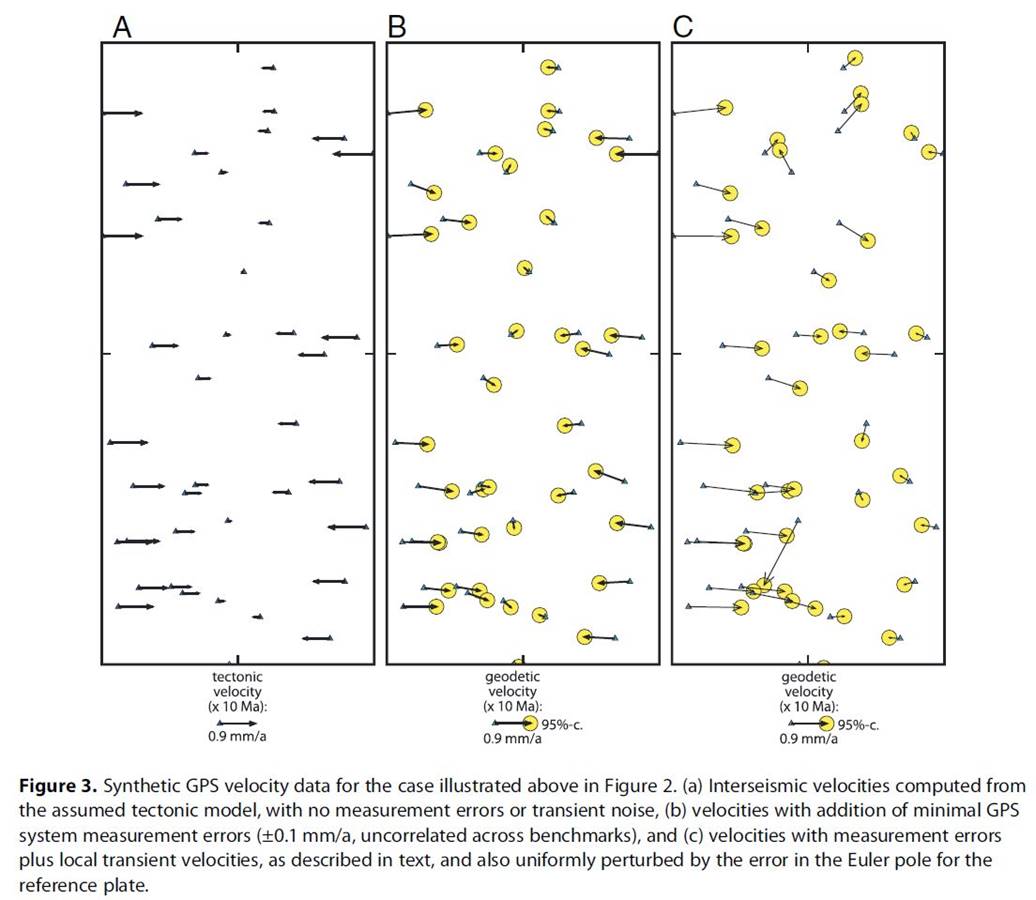
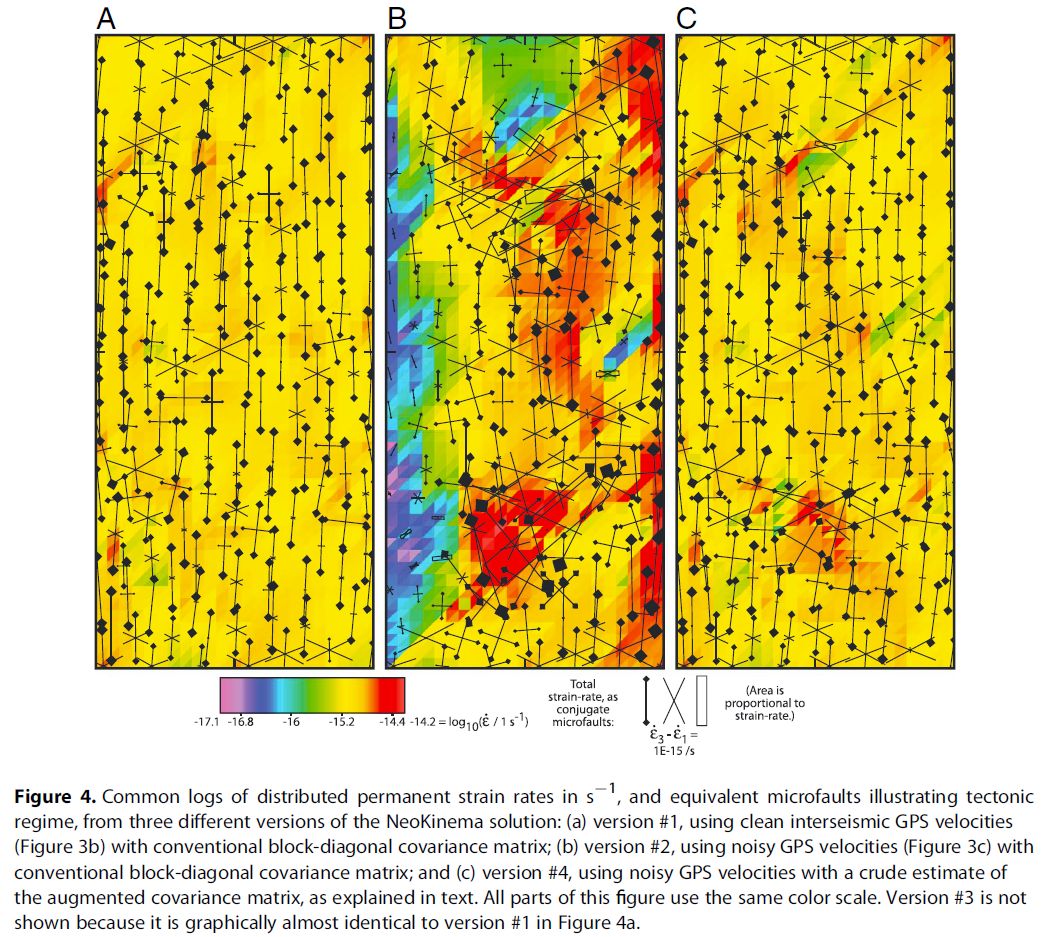
Abstract. GPS geodesy provides very precise velocities of benchmarks on decadal timescales, and geodesists often describe their uncertainties with a velocity covariance matrix. However, those who model neotectonic deformation to estimate long-term seismic hazard want constraints on the interseismic velocities of stable bedrock on multi-thousand-year timescales. When the former (available data) are used as proxies for the latter (desired constraints), it is necessary to increase uncertainties to characterize a variety of transient and/or surficial noise processes, including magma chamber recharge, postseismic relaxation, pore fluid motion, extremely slow landsliding, and glacial isostatic adjustment. The effects of transient noise on distant reference benchmarks also add to uncertainty of the long-term velocity reference frame. We augment the reported velocity covariance matrix with transpose products of velocity perturbation vectors from simple models approximately describing anticipated transient and surficial noise sources. No artifacts are introduced by this method because the velocity-vector data are unchanged. When the inverse of the augmented covariance matrix (the “diminished normal matrix”) is used in the objective function of a neotectonic deformation model partially driven by GPS data, the perturbing effects of transient and surficial signals are greatly reduced. Improvement occurs even when the prior estimates of noise processes are rather crude. We present two examples computed with synthetic data.
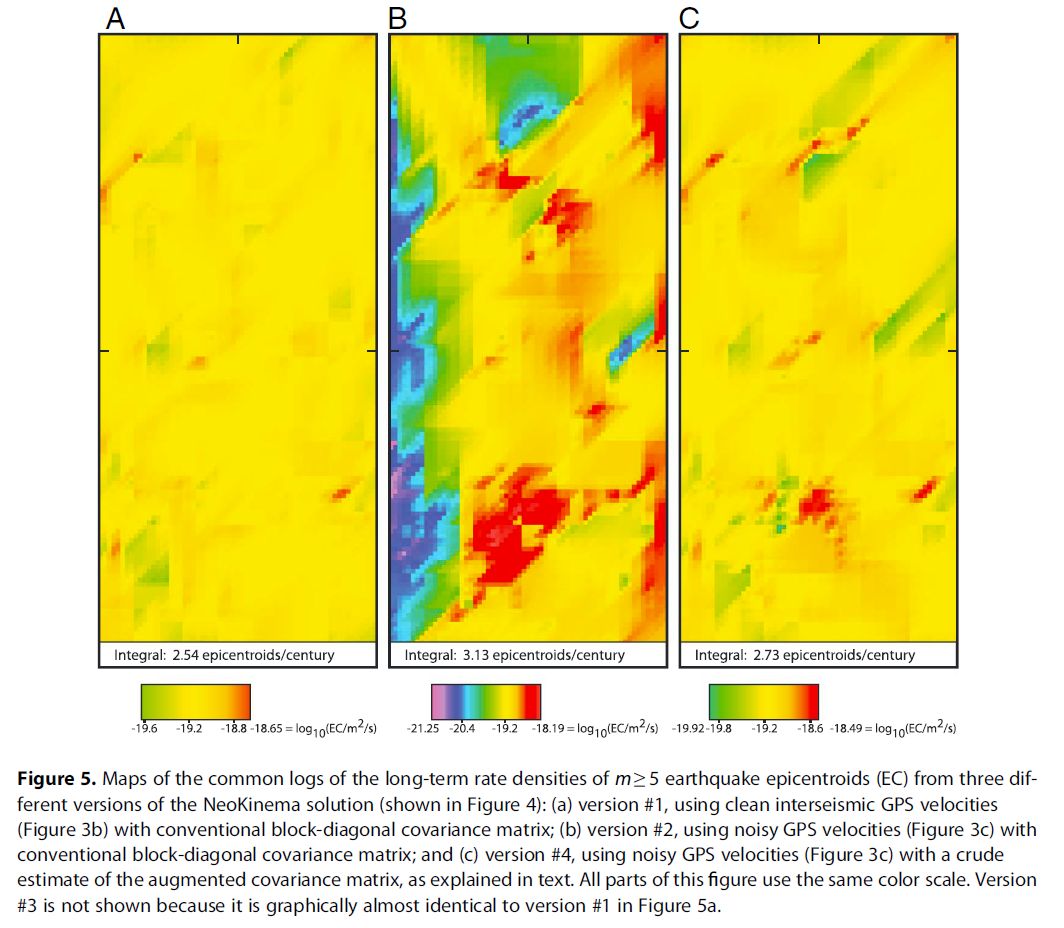
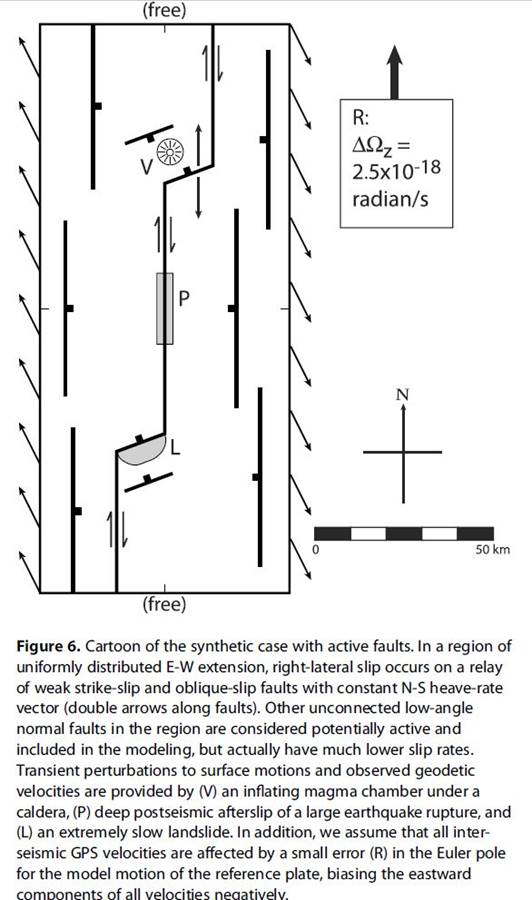
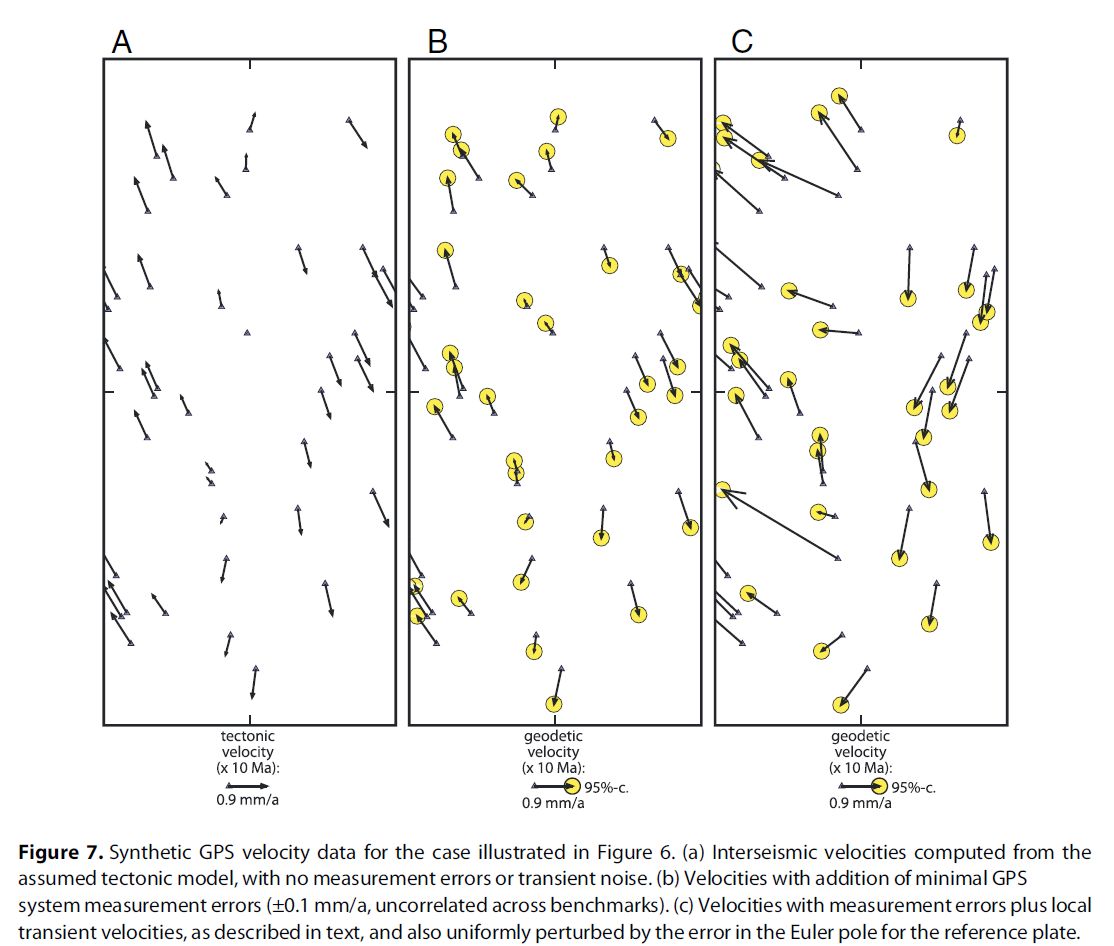
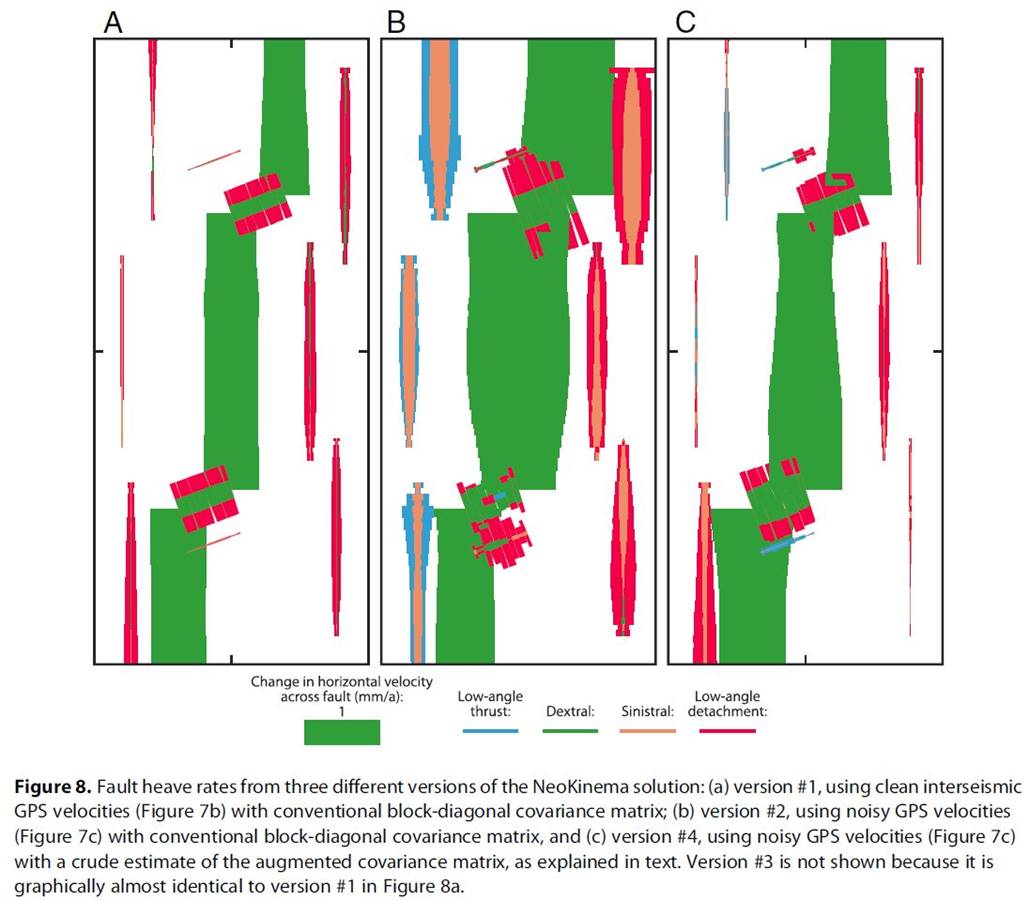
Erratum: NeoKinema version 5.0 (and earlier) contained a bug which was activated in problems where the user supplied a .GP2 velocity covariance matrix as part of the input, as we did in Versions 3 & 4 of each sample problem in this paper. The result of the bug was to report an N2 (RMS, or root-mean-square) measure of the GPS velocity misfits at benchmarks which is inaccurate, and too low by roughly 30~42% (but possibly more inaccurate in special cases). Users of NeoKinema are encouraged to download version 5.1 or 5.2 (or later) in which this bug has been fixed. Below we show how 4 numbers reported in Table 1 and Table 2 of this paper should be corrected. Fortunately, each solution presented in the paper was otherwise valid, and this error in scoring had no effect on our main arguments. PB 2017.10.30
In Table 1, Alternative Versions of the Synthetic Model Without Faults:
|
Version # |
1 |
2 |
3 |
4 |
|
GPS Misfit, |
0.428 |
1.895 |
0.475 |
0.653 |
In Table 2, Alternative Versions of the Synthetic Model With Faults:
|
Version # |
1 |
2 |
3 |
4 |
|
GPS Misfit, |
0.853 |
3.138 |
0.856 |
1.682 |
Postscript#1. This paper demonstrates that one can obtain a better neotectonic model from NeoKinema (or similar kinematic inverse code) by anticipating the likely patterns of non-tectonic and non-stationary noise in GPS data, and building that information into an augmented covariance matrix. A natural follow-up question is, Can we use the residuals from the NeoKinema solution to obtain posterior estimates of those noise processes? The answer is yes, but some additional linear algebra is required. To do this, we have now created a new code, GPS_Postprocessor2, which estimates the actual amplitude of each noise process separately (including any bias in the velocity reference frame). This new code requires a log-file from the original application of preprocessor GPS_Covariance, plus the files used or created by NeoKinema. It produces a report in text format, plus 3 maps (in Adobe Illustrator .AI format) of 3 distinct parts of the residual GPS misfit velocities: (1) those due to reference frame discrepancy; (2) those due to anticipated noise sources; and (3) other residual misfits which are not understood. PB 2017.11.14
Postscript#2. CAUTION: We have recently discovered some cases in which our method of augmented covariance leads to over-correction of geodetic transients by ~50%, causing errors in the long-term tectonic model which are opposite in sign (but smaller in magnitude) compared to the errors that would have occurred without augmentation. This problem can occur where: (a) the tectonic model is dependent on geodetic (as opposed to geologic) data to indicate the proper map-pattern of long-term deformation; and (b) the spatial pattern of transient velocities resembles a temporary amplification of long-term tectonic velocities. Examples of case (b) include post-seismic after-slip and/or viscoelastic relaxation. Therefore, we no longer recommend our method of augmented covariance as the optimal method for dealing with post-seismic after-slip and/or viscoelastic relaxation. Where these are suspected, it may be preferable to either: (1) create a quantitative model of the transient [e.g., E. Hearn, 2022, Seismological Research Letters, 93, 2973-2989, doi: 10.1785/0220220156] and subtract it from the geodetic velocities to be used for long-term tectonic modeling; or (2) simply edit the affected benchmarks out of the geodetic dataset to be used for long-term tectonic modeling. PB 2023.03.15