31. Bird, P. and X. Kong [1994] Computer simulations of California tectonics confirm very low strength of major faults, Geol. Soc. Am. Bull., 106 (2), 159-174.

Abstract. Recent improvements in the technique of modeling fault networks with thin-plate finite elements yield full convergence of the solutions, without any compromise in the representation of the frictional rheology of the upper crust or the transition to dislocation creep in the lower crust.

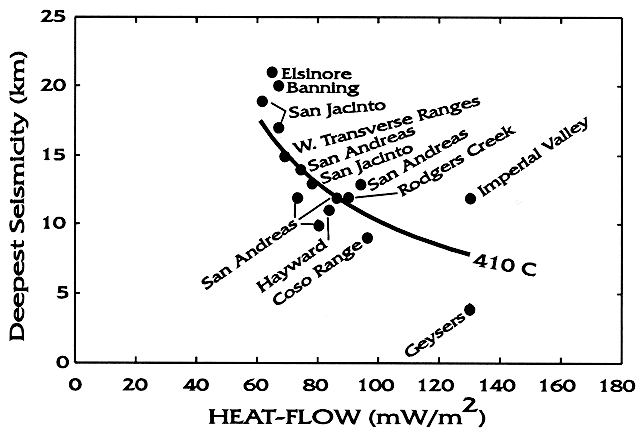
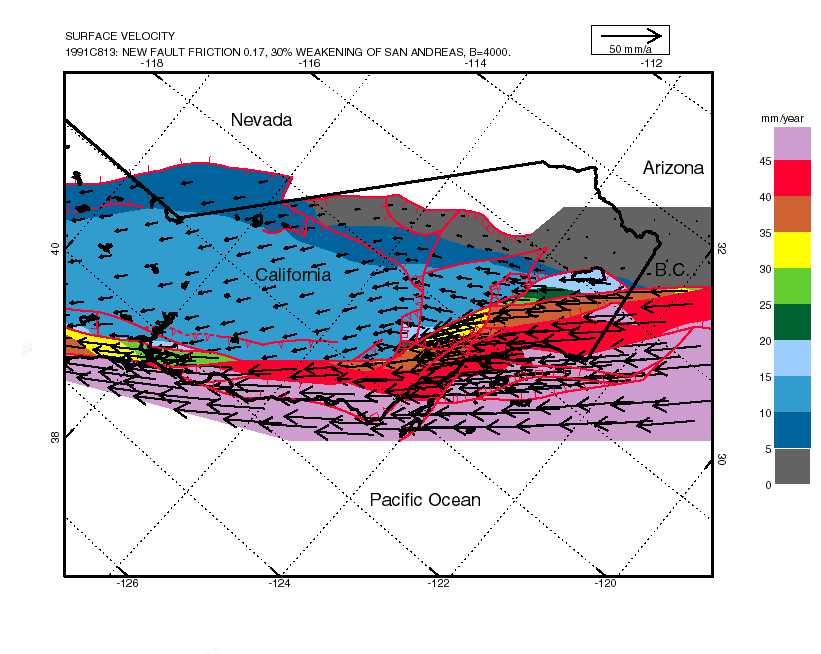
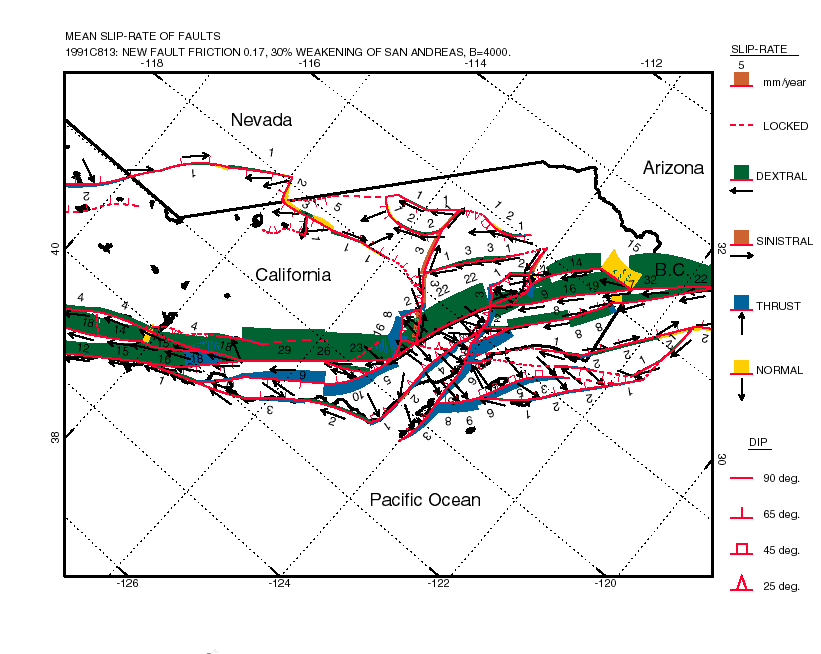
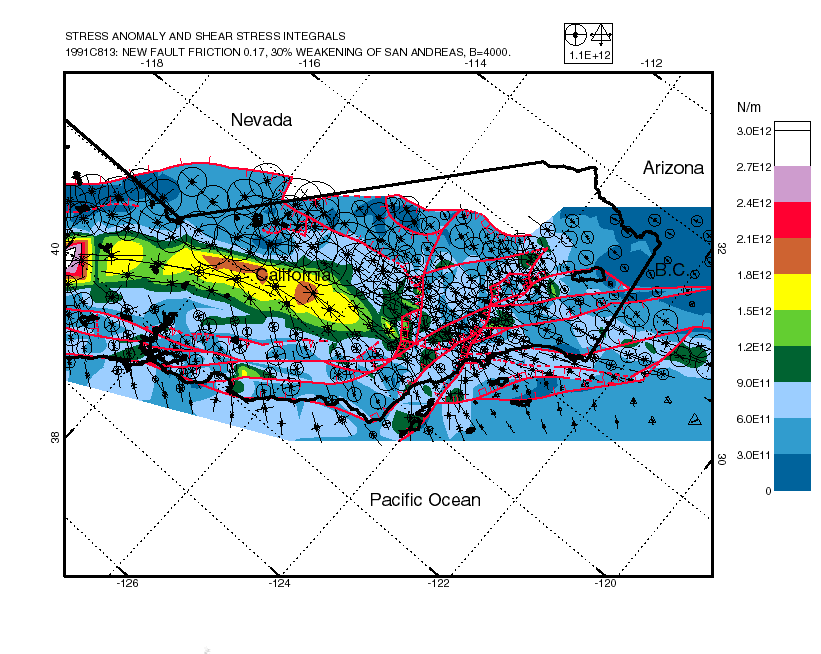
We apply these techniques to model the California region, incorporating all faults with estimated slip rate over 1 mm/yr, as well as variations in elevation, heat flow, and crustal thickness. Velocity boundary conditions on the model sides are based on the NUVEL-1 plate model and an approximation of deformation in the Great Basin. The frictional and dislocation-creep rheologic constants of the crust are calibrated to reproduce the observed variations in the maximum depth of seismicity, which occurs at model temperatures of 350-410° C. This leaves two free parameters: the (time-averaged) coefficient of friction on faults, and the apparent activation energy for creep in the lower crust.

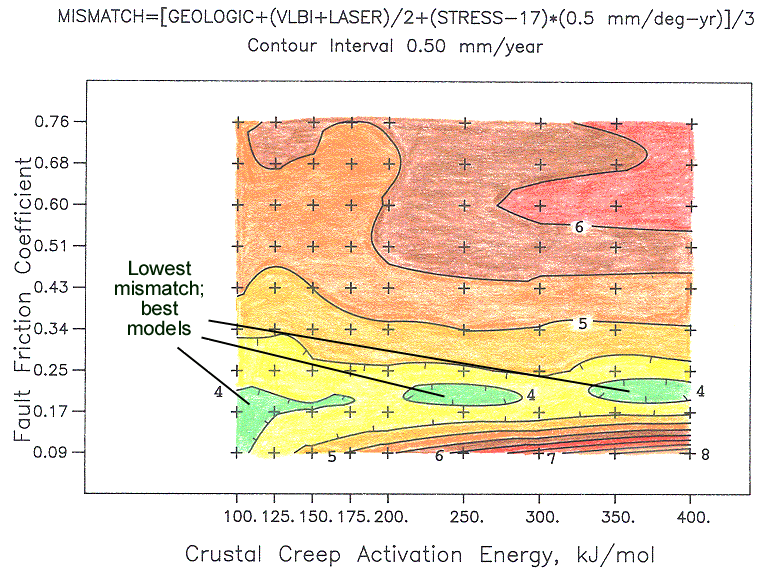
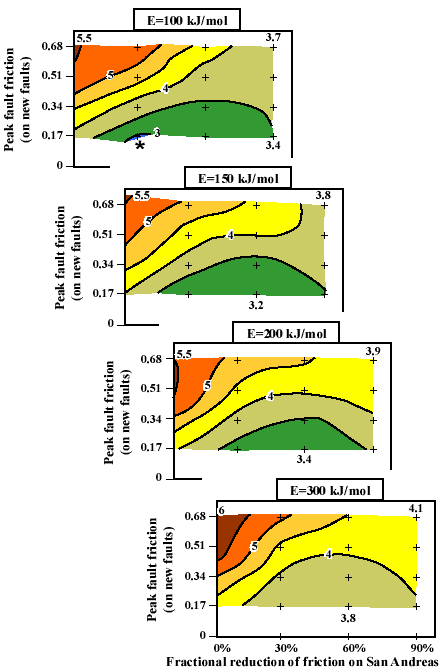
These parameters are systematically varied in three sets of 10, 81, and 64 experiments, respectively. The predictions of each model are tested against three published data sets: a set of 79 geologic limits on average slip rate on faults, a set of 221 principal stress directions, and a set of 841 secular rates of geodetic baseunes (both trilateration and VLBI [very long baseline interferometry]). The patterns of model scores indicate that the time-averaged friction coefficient of major faults is only 0.17-0.25, or only 20%-30% of the value (0.85) that is assumed for the friction in the intervening blocks. (The laser trilateration data taken alone would indicate a preference for a high-stress model, but this model is one with very little fault slip and seismicity, which can be rejected on other grounds.) In the final three-parameter set of 64 models, we test whether the anomalous weakness of faults is uniform or proportional to net slip. With slip-dependent weakening, there is a general reduction in prediction errors, which supports the hypothesis. The geologic data and geodetic data agree in implying that fault weakness (that is, friction of 0.17) is general, with an additional 30% slip-dependent weakening of the San Andreas (to friction of 0.12, or 14% of normal). The stress data, however, are fit best if all weakness is slip-dependent (effectively, only the San Andreas is weak). Thus, the hypothesis that all weakening is slip-dependent should not be rejected.

The best models predict all available data with RMS (root mean square) mismatch of as little as 3 mm/yr (6% of the relative plate velocity), so their predictions may be useful for seismic hazard estimation, at least along faults where no data are available.

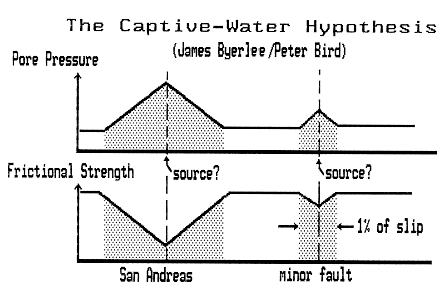
This study extends the finding of very low friction from subduction zones, where it was previously documented, to a dominantly strike-slip system in which underthrusting of wet sediment is not widespread. Return of previously subducted water from the mantle and its chemical or physical binding in fine-grained gouge are possible explanations for the very low friction.

P.S. For more attractive graphical presentations of this model, see: R.W. Simpson [1997] Quantifying Anderson's fault types, J. Geophys. Res., 102(B8), 17909-17921.  For more up-to-date models of the San Francisco Bay area, using the same program, see: E.L. Geist and D.J. Andrews [2000] Slip rates on San Francisco Bay area faults from anelastic deformation of the continental lithosphere, J. Geophys. Res., 105(B11), 25543-25552.  For my current best estimate of California neotectonic flow, see Bird [2009, J. Geophys. Res.].  (This paper remains posted because it may have continuing value as a demonstration of the surprising weakness of faults in California.)   P. Bird 2010.04.09