Step 17: Obtain GPS-velocity covariance matrix and put into .gp2 format?

What is the GPS-velocity covariance matrix?

In general, any covariance matrix is a powerful tool for expressing what remains uncertain about a group of variables that have already been measured many times.
This tool can be applied to help make smart decisions about systems which are messy and complex because they have many different kinds of uncertainty piled on top of each other.

However, before we get into matrix-notation and double-subscripts, let’s review the definitions of variance and covariance using an example of a much simpler (but real) system, with only two measurements per day.
Let x be the daily maximum temperature in downtown Los Angeles, and let y be the daily maximum temperature in downtown San Francisco.
Each is measured every day and recorded, and we can use a subscript to identify the day: x₁, x₂, x₃, …, x_N. Since temperatures have been measured since about 1850, N is about 61,000.
The mean of x is defined as: 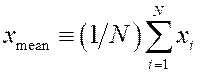, and the mean of y is defined as: .

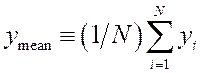In this particular case, we notice that x_mean > y_mean and that the units of the means are temperatures [°F or °C].
The variance of x is defined as: 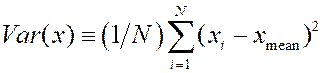and now its units are temperature-squared [(°F)² or (°C)²].

Because variance is based on a sum-of-squares, it can never be negative.
In exactly parallel fashion, the variance of y is defined as: 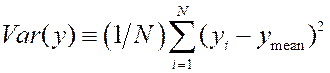, and this is also in units of temperature-squared. It can also never be negative.
Finally, the covariance of x and y is defined as: 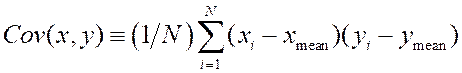  , which is also in units of temperature-squared.
An interesting new feature of   is that it is not necessarily positive; in theory it could be negative
(if temperatures in San Francisco actually go down on days when they go up in Los Angeles—but that is probably not the case!).
Now we might notice a fairly trivial relationship between variance and covariance:   for any variable x.
So, covariance is the more general measure (including variance as a special case).
That is why we usually talk about the “covariance matrix” rather than talking about the “variance-covariance matrix” as some people do.

Because of the conceptual awkwardness of squared units [e.g., (°F)² or (°C)² in our case], some people don’t like to talk about variances and covariances; they may prefer other quantities derived from them.
For example, the standard deviation of x is the square-root of its variance, , which brings it back to physical units of temperature [e.g., °F or °C in our case].
And, the correlation coefficient of x and y is just 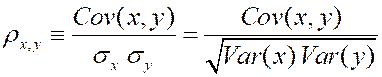, which is dimensionless, with values in the possible range of .

However, the great advantage of using variances and covariances lies in the well-known principle that:
(Co)variances contributed by independent processes are additive.
This rule allows us to apply simple but powerful methods of linear algebra to covariance matrices.
No equivalent simple rule would be available if we worked with standard deviations, or with correlation coefficients!

Before we leave this simple system, let’s apply our general knowledge about the world to make some observations about , , and in this particular case:

· In the early days of measurement (19^th century), measurement errors were pretty large, and measurement-related variance probably made up a significant fraction of these (co)variances. However, after continual progress in standardizing thermometers, standardizing the housings that hold them, standardizing the placement of these housings inside the city, and standardizing the timing and methods of recording, measurement noise has been greatly reduced. Its standard deviation is probably no more than ±1 °F today, contributing measurement-variance of 1 (°F)² or less to (co)variances. So, in recent years most of the (co)variance that we see is coming from “real” natural variations, rather than from measurement-variance.

· These natural variations occur on a variety of time-scales. Daily variations result from sunrise and sunset. Week-scale variations are due to weather fronts passing through. Seasonal (year-scale) variations are due to Earth’s orbit and the relative inclination of its rotation axis. Multi-decade-scale variations are caused by greenhouse gasses and global warming. And even longer, multi-thousand-year-scale variations are probably associated with ice ages and interglacial epochs (although the causes of these are still somewhat mysterious).

· Because of these many time-scales of natural variation, (co)variances measured over just a short time (e.g., in one week; N = 7) are not likely to be representative of longer-term (co)variances. They would be formally-admissible estimates of the long-term (co)variances, but they would not be very good estimates! The most likely case is that very short-term estimates of (co)variances are under-estimates, or lower-limits.

Next, let’s talk about the ways in which measuring covariance of interseismic GPS velocities at many benchmarks is different from our simple city-temperature case:

· Horizontal velocity is a 2-component vector; is a common way of expressing it. Since we are now measuring 2 things at each benchmark, there is a tiny 2×2 “tile” sub-matrix of (co)variances associated with each benchmark. Its top-left component is for that benchmark; its lower-right component is ; and, its upper-right and lower-left components are equal to each other: . So, this (symmetric) tile has exactly 3 degrees of freedom, and the information it conveys is exactly the same as the information conveyed by the 3 quantities (columns) [, , Correlation] associated with that benchmark (row) in the .gps file. The numbers are not the same, because these two representations use different measures with different units, but the information is the same.

· What a GPS-velocity covariance matrix (or .gp2 file) adds is the covariance of each horizontal velocity component at one benchmark
with each of the horizontal velocity components at all the other benchmarks.
To do this, it has to include every possible pair of benchmarks.
Thus, the size of the matrix (measured in tiles) is B rows × B columns, where B is the number of benchmarks.
Or, in terms of numbers, the matrix size is 2B rows × 2B columns, containing 4B² numbers altogether.

· Unfortunately, the horizontal velocity of a benchmark cannot be measured in a day! Due to intrinsic variability in Earth’s ionosphere, interfering radio signals, clock errors, etc., it actually takes about a decade to measure the horizontal velocity components of a benchmark to within a “useful” standard deviation of ±1 mm/a or less. This means that our present datasets give only N £ 1 for most benchmarks, and only N £ 3 for the oldest and best! So, the numbers that make up a GPS-velocity covariance matrix are NOT actually calculated (with the simple formula above) from a long historic record. (To do this, we would have needed the assistance of angels with infinite lifetimes and infinite patience, who would have made measurements of GPS-velocity over 1,000 to 10,000 years, giving N = 100 ~ 1000.) Instead, the actual numbers in GPS-velocity covariance matrices are theory-based MODELS of the (co)variances we expect across longer times, based on more-easily observable quantities like minute-to-minute, hour-to-hour, and day-to-day variations in apparent benchmark position. It also follows that these THEORETICAL MODEL (co)variances are mostly or wholly composed of velocity-measurement variances, and do not adequately sample the other velocity-variance contributions that come from “real” time-dependence of crustal velocity. Thus, the magnitudes of their numbers are almost always under-estimates or lower-limits on the real magnitudes of the long-term velocity covariances. [In Step 19, I will discuss how this problem can be partially corrected.]

To conclude this introduction to GPS-velocity covariance matrices, let me list a few “cheerful facts” about them:

1. These matrices are always exactly square (with equal numbers of rows and columns).

2. These matrices are always exactly symmetrical (because by the definition formula).

3. The numbers in these matrices are real numbers in units of (velocity)². (If the units are (mm/a)², then the magnitudes of the numbers are likely to range from 0.01 to 100 (mm/a)².
Or, if the units are SI units of (m/s)² = (m²/s²) = (m² s^-2), the magnitudes of the numbers are likely to range from 1.E-23 m² s^-2 to 1.E-19 m² s^-2.
Do not confuse these apparently-small numbers with zeros!)

4. The numbers on the diagonal (where row# = column#) are always positive.

5. The numbers off the diagonal may be positive, negative, or zero.

6. The magnitudes of numbers off the diagonal are never more than the geometric mean of the corresponding two diagonal numbers: .

7. The eigenvalues of any GPS-velocity covariance matrix should all be positive (or, something about it is defective).

How can I get a GPS-velocity covariance matrix for my study area?

You cannot (and should not try to) compute it for yourself. At minimum, you would need access to all the minute-by-minute position determinations for every benchmark over all the years. Such datasets are too big to be portable. Also, you would need theoretical and practical training to understand how the different variance components behave and add up.

Typically, you contact the geodetic expert(s) who computed the solution that you converted into your .gps file (in the previous Step), and ask them, very nicely. Or, you might offer to pay them for their time, if they need to create it just for you.

Sadly, such covariance matrices are rarely published (except as links on web sites), and little-discussed. This is probably because they are:

· Very large matrices (far too big to print on a two-page spread in a journal);

· In abstract units of (velocity)², which casual readers have trouble understanding;

· Often dominated by their diagonal-tile components (whose information is already available in .gps format); and

· Difficult to visualize. (Actually, selective visualization is straightforward: Plot some map-views of benchmark locations with velocity-variation vectors consisting of “prominent*” eigenvectors, each multiplied by the square-root of the *corresponding large eigenvalue.)

If you ARE successful in obtaining a GPS-velocity covariance matrix:

Be sure that you acknowledge the expert(s) who provided the matrix, in any seminars, manuscripts, and/or proposals you write!

Be sure that you understand the units of the floating-point numbers: (mm/a)², or (m/s)², or something else? Ask if necessary.

Be sure that you understand how the two horizontal velocity components are ordered at each benchmark: as , or as , or something different? Ask if necessary.

Be sure that you understand how the benchmarks are ordered within the rows and columns of the covariance matrix? Is it the same as ordering in your .gps file, or something different? Ask if necessary.

Then, based on all this understanding, write a short utility program (in your preferred programming language, or in a spreadsheet) to convert the GPS-velocity covariance matrix to my .gp2 format, explained here.

Return to your NeoKinema-parameter file (introduced in Step #8; sample file is parameters_for_NeoKinema.nki.txt)
and open it with a plain-ASCII text editor such as NotePad or EditPad Pro.
In line #17, replace the name of the .gp2 file (“WUSC002.gp2”) with your actual filename.

If you are NOT successful in obtaining a GPS-velocity covariance matrix:

Actually, there are several compensations for your disappointment:

· You are now free to sort the benchmarks (rows) in your .gps file, and to delete any that you don’t want or need. In particular, you should delete any benchmarks whose horizontal velocities appear to be affected by coseismic and/or postseismic movements around a large shallow earthquake, during (or just before) the GPS measurement time-window.

· If you run NeoKinema WITHOUT using a .gp2 matrix, it will run more quickly and use less computer memory.

· A lot of the “power” or “value” in a .gp2 matrix is actually in the diagonal tiles, and that information is already captured in your .gps file.

· If you decide to build a long-term model .gp2 file (including both measurement-variance and natural-variance components), you will still be able to do so, as described in Step 19 of this Guide. (It’s just that the measurement-variance part of your model will be less complete and accurate than would be ideal.)